
Imagine a digital-audio encoding and decoding system that delivers far better sound quality than that of any previous analog or digital technology, including 192kHz/24-bit and quad-rate DSD. Now imagine that this system’s bit rate is between 0.8 and 1.5Mbps, down to one-tenth that of conventional “hi-res,” allowing it to be streamed or downloaded in standard FLAC or Apple Lossless file formats. Finally, consider the possibility that this system would be based on a single file format that is backward compatible with existing delivery systems and playback devices, from smartphone streaming to downloads that feed the highest of high-end home DACs.
Sound like an impossible dream? Read on, and I’ll show you how Meridian’s Master Quality Authenticated (MQA) pulls off this remarkable feat.
MQA in Practice
Before getting into the technical aspects of MQA, let’s review the basics. Master Quality Authenticated is an innovative and sophisticated new method of encoding digital audio that simultaneously improves fidelity and lowers the bit rate. It’s a suite of technologies that addresses the limitations of conventional digital audio by rethinking the entire chain, from acoustic source to playback device. It was developed by Meridian Audio co-founder Bob Stuart and longtime collaborator Peter Craven of Algol Applications.
In practice, MQA is delivered to listeners as a conventional lossless file, such as FLAC or Apple Lossless at 44kHz or 48kHz at 24 bits. If you play the file though a DAC without an MQA decoder, you’ll hear better-than-CD sound quality. If you play the file through a DAC with MQA decoding, you’ll hear the sound in the studio’s original bit rate, which could be anything from 44.1kHz to 384kHz (or higher), provided that your DAC can handle the studio’s sample frequency. This single-file hierarchical aspect of MQA has important implications for the technology’s adoption by record companies and content distributors.
The decoder can be implemented in many ways—partly integrated into a DAC chip, or as a bit of software in a phone, for examples. Every decoder will indicate to the listener when an MQA file is playing. Here’s where the “Authenticated” part of Master Quality Authenticated comes in; the MQA light or icon assures that what the listener is hearing on playback is exactly what the engineers heard in the studio. How does this happen? MQA ties the studio’s analog-to-digital converter and the listener’s digital-to-analog converter into what is effectively a single system. In addition, MQA’s rich metadata carries information about the particular analog-to-digital converter and encapsulation used to make the recording or transfer so that the decoder can play it back correctly. And if the decoder knows what DAC it’s driving, it can also optimize its sound. This is why MQA can claim to authenticate the studio experience for the listener.
As of this writing, more than fifty companies—from major players to niche high-end firms—plan to support MQA with compatible playback devices. Meridian has already launched its first MQA-capable DAC, the $299 Explorer2. The lossless streaming service Tidal is behind MQA in a big way; it will begin streaming MQA files in Q2 of this year. MQA allows Tidal to give its customers real high-resolution streams in a format that fits Tidal’s existing distribution infrastructure. In an e-mail exchange, Pål Bråtelund, Strategic Partnership Manager at Tidal, said: “At first, I thought the last thing the industry needed was another codec. But then Bob [Stuart] played some recordings I knew extremely well, and I instantly understood that MQA may be what makes people talk about great recordings and great music rather than about ‘hi-res.’”
For Tidal, and also for the world’s record companies, MQA solves the big problem of multiple inventories for different playback applications. A single MQA file works for every listener on every device. This backward compatibility and single inventory are powerful incentives for record companies and content distributors to adopt MQA—quite apart from the improved sound.
So now let’s address that confounding issue of just why MQA sounds better than any other format extant, and how it can do so at such low bit rates.
Overview
First, a disclaimer: This description is by no means a full assessment of MQA. The technology incorporates teaching from fields as diverse as psychoacoustics, neuroscience, brain imaging, and information theory that are beyond my ken. A full explanation could fill a book.
MQA doesn’t tinker at the margins of digital audio’s limitations, but rather represents a departure from current thinking. Despite its radical approach, it operates within the domain of the existing technological and commercial digital-audio infrastructures.
The seemingly insurmountable barriers to better digital sound have been circumvented through elegant and imaginative thinking. For example, MQA—astonishingly—rethinks sampling and quantization (those twin pillars of digital audio) by implementing groundbreaking new sampling and quantizing techniques. Once inviolable “laws” of sampling theory, such as “a sampled system cannot convey time differences shorter than two sample periods,” are exposed as merely the conventional wisdom of an earlier age. Similarly, MQA reconsiders another cornerstone of digital audio, the brickwall filter. Meridian has developed a more sophisticated analysis of digital filtering, and of the aliasing the filter is designed to prevent.
The description below is thus a small sliver of the technology behind MQA—a sliver that on its own would be cause for celebration. But understand that, combined with other advances that are beyond the scope of this article, MQA is a revolution that comes along once in a lifetime. For this article I’ll explain just two aspects of MQA: one of the reasons it can sound better than any current “high-resolution” PCM or DSD system, and how an MQA file can convey that extraordinary sound quality in a stream roughly one tenth the size of conventional “hi-res” PCM. (For the technically minded, Stuart and Craven’s Audio Engineering Society paper explaining several aspects of MQA, “A Hierarchical Approach to Archiving and Distribution,” can be purchased from the Audio Engineering Society at aes.org, paper #9178.)
Temporal Blur
In my view, MQA’s most important characteristic is not that it can deliver high resolution at a low bit rate (although that aspect is what will gain it widespread adoption), but rather that it sounds better than any other format extant, analog or digital. Meridian maintains that the standard metrics for digital audio—sample rate and the number of bits in each sample—are far less important than two new metrics: 1) absolute stability of the noise floor and 2) the amount of “temporal blur” in the digital system. This last term describes the smearing of transient information over time by digital filters. Temporal blur affects the sounds’ timing precision. That is, music’s transient’s energy is spread out, appearing before and after the transient. Meridian has previously addressed this problem of filter “ringing” with its “apodizing” filter, a technique now commonly used. The apodizing filter doesn’t remove ringing (temporal blur); rather, it kills the incoming ringing and replaces it with its own ringing that occurs only after the transient, which is less sonically detrimental. MQA’s new techniques outright remove temporal blur rather than making it less sonically objectionable.
The steeper the filter, the greater the temporal blur. The higher the sample rate, the less steep the filter needs to be. This is one of the reasons why conventional high-sample-rate digital audio sounds better than standard-rate—the filters are less injurious.

If Meridian were forced to characterize the quality of a digital audio system with a single metric, it would be how much temporal blur the system adds, measured in microseconds or milliseconds. Fig.1 is a chart showing the amount of temporal blur for various audio formats. MQA (shown as the red line) reduces temporal blur to about 10µs, roughly 30 times lower than the temporal blur of regular 192kHz/24-bit PCM, and much lower than that of CD.

Fig.2 shows the respective impulse responses of typical 192/24 and MQA. The narrower the impulse, the less temporal blur. MQA achieves this with a new approach coupling sampling with reconstruction, and, surprisingly, recognition that the very aliasing that the filter exists to prevent can, under certain managed conditions, be less harmful than the filter itself. Another innovation is selecting the filter’s characteristics based on the song or piece of music. By contrast, conventional digital filters tend to be fixed for “worst-case scenario” signals, as well as exemplifying the view that any aliasing is unacceptable.
Meridian’s pursuit of techniques to increase timing precision was inspired by recent findings in psychoacoustics and neuroscience. The temporal blur target of 10µs is based on this research. The AES paper mentioned earlier is full of citations to psychoacoustic and neuroscience literature. Timing is so important because our hearing mechanism is acutely tuned to impulsive sounds for instantly determining the “where, then what” of the object creating the sound. The distortion of these vital cues by temporal blur diminishes the sense of musical realism in a variety of ways. In the accompanying interview, Bob Stuart describes in more detail why temporal blur is so detrimental to sound quality.
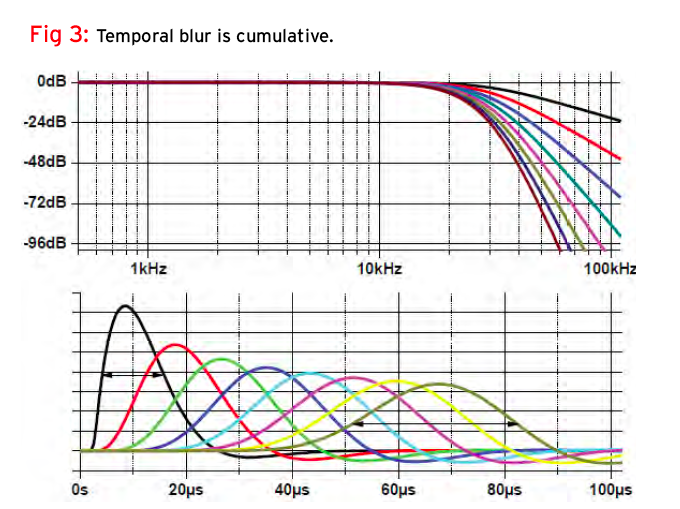
However, improving the temporal response of the digital chain also places tighter requirements on the analog system. In a typical recording chain we have a microphone, amplifier, recording console, A/D, D/A, playback amplifier, and loudspeaker. To approach the target transparency of air, each step must be right and work towards this end. As Fig. 3 shows, temporal blur is cumulative; each successive stage can inadvertently spread transient energy over a wider and wider interval. It’s not uncommon for a signal to have been subjected to a cascade of eight filters by the time it’s gone from microphone to loudspeaker; the damage is significant, and yet each individual stage isn’t that bad in isolation.
Rethinking the Container
To understand how MQA can convey true high-resolution digital audio at a much lower bit rate, you must first realize that a large percentage of a conventional 192kHz/24-bit file is empty baggage that contains no useful information. A 192/24 file is like a microwave-oven-sized box storing an object the size of a paperback book.
One reason conventional PCM coding is so inefficient is that the sampling frequency is fixed, determined by the highest audio frequency we want to encode. The Nyquist Theorem says that the sample rate must be at least twice as high as the highest audio frequency of interest. A digital system’s fixed sampling frequency is chosen to accommodate the highest audio frequency we want to preserve—44.1kHz sampling to encode a 20kHz audio signal, for example. A fixed sampling frequency is applied to all audio signals, no matter their frequency. It’s illuminating to consider that a 20Hz audio signal is sampled about 2200 times per waveform, whereas a 20kHz audio signal is sampled slightly more than two times per waveform.
MQA addresses this disparity by losslessly (or virtually) dividing the audio into octave-wide sub-bands, conceptually coding each with a lower sampling rate than the ensemble. MQA is truly hierarchical, and although the example here is 192kHz, sample rates of 384, 768, or higher are accommodated. In fact, the mathematics includes infinite sampling (analog) since that is the real target.
Similarly, in conventional PCM, the quantization word length is typically fixed at 16 bits, 20 bits, or 24 bits. (The word is a binary number that represents the analog signal’s amplitude at the moment the sample is taken.) The longer the word, the more bits available to encode the amplitude information, and the greater the dynamic range that can be captured. However, there is a large inefficiency because the steps are linear and not logarithmic. MQA, by contrast, uses fractional bits to more accurately code the critical kernel.
The term “coding space” describes the entire range of frequencies and amplitudes that can be captured by the encoding scheme. Fixed sample rate and fixed word length give us a coding space that is rectangular. For example, in a 192kHz/24-bit system, we can encode audio frequencies up to 96kHz (half the sampling frequency) with a theoretical spectral dynamic range of 144dB. This coding space is “rectangular” because plotting the system’s frequency range along the horizontal axis and the dynamic range along the vertical axis results in a rectangular box and if the frequency axis is linear, area maps to data rate.


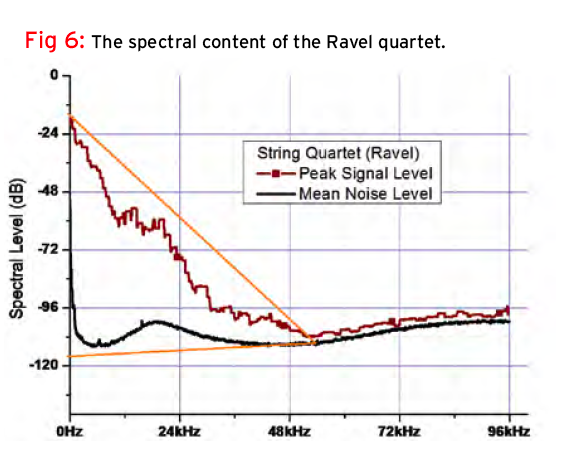
But the actual “information space” of sounds in nature and music isn’t rectangular; it’s triangular like that of Figs. 4 and 5. As frequency increases, amplitude decreases. Fig. 6 shows a triangle superimposed on the spectral content of an actual musical signal (the Ravel quartet). The bottom of the triangle defines the recording’s noise floor. Meridian analyzed the spectral content of thousands of recordings across all musical genres and confirmed similar spectral distributions, each one different, but of a class.
MQA encodes the information within the triangle as precisely as possible using advanced sampling kernels. Moreover, it effectively does this with different rates from the perspectives of the original and reconstructed signal compared to the transmission path.
Very high frequencies can be preserved with word lengths that reflect their narrow dynamic ranges, since above the point of the triangle there is no signal, just (inaudible) noise. In fact this region is a paradox: It contains no music, but if we remove it by filtering we would blur envelope information in the octave below. Audio information above 20kHz has very little amplitude—it consists of low-level upper harmonics but is critical to reproducing the timing that cues location. Consider that the fundamental frequency of the highest note on an 88-key piano is 4186Hz. An analog-to-digital converter would never encounter full-scale signals at 96kHz, yet the conventional 192/24 PCM system is designed to encode signals that it will never see.
In short, the combination of folding the sample rate linearly with an encoding kernel that reflects the signal greatly reduces the number of bits required to correctly capture the entire musical signal.
I must stress that this approach has nothing in common with lossy compression systems that throw away information inside the triangle deemed to be “inaudible” because those sounds are theoretically below the instantaneous human auditory masking threshold. Rather, MQA applies bits precisely where they are needed and doesn’t allocate data to potentially encode signals that will never exist. By comparison with MQA, conventional PCM is a crude and inefficient method of encoding audio. Well-meaning but uninformed skeptics, to whom large file size is the ultimate measure of resolution (and a source of comfort), may suggest that MQA ignores real musical information in its quest to reduce the bit rate. Not true: There is no musical information outside the triangle, and all the information within the triangle is preserved. Nothing is thrown away as with lossy compression systems. In fact, the signal heard in the studio is delivered and authenticated with lossless bit-for-bit precision to the listener.
Encapsulation and Musical Origami
Now we have an extremely high-resolution file (by virtue of the reduced temporal blur, advanced sampling and quantization methods, and other techniques) with a much smaller file size than one generated by 192/24 encoding. How can that file be compatible across all playback platforms, from a 44.kHz/16-bit smartphone to a state-of-the-art, five-figure, high-resolution DAC at the front end of a reference-grade home system?

The answer is in the technique Meridian calls “Encapsulation.” Look at Fig. 7, the coding space of 192/24 with the triangle superimposed in orange over the Ravel quartet we saw in Fig. 4. The red line is the music signal’s peak spectral content, the blue line the recording’s noise floor. The enclosed area within the orange triangle is equivalent to 900kbps peak/channel (around 900kbps average for two channels). Encapsulation captures and protects this region. Incidentally, you can see from this illustration that if we have to reduce the coding area to one-eighth (to fit two channels into MP3 or AAC at 192kbps), a lot of the music inside the triangle would be removed.
The signal space is divided into three areas: A is the frequency band up to 24kHz, B spans 24 to 48kHz, and C is information and noise from 48 to 96kHz. Above 55kHz, the signal has fallen below the background noise, so C is mostly an artifact of the original sampling or recording system—the paradox I referred to earlier.
Encapsulation takes the information within the triangle that falls within Area C and “hides” it beneath the noise floor of the recording in Area B. So any information we care about that was within Area C (within the small point of the triangle that protrudes into Area C) is now encoded and buried beneath the noise floor in Area B.

Taking this concept a step further, audio signals within the triangle of “B” (audio frequencies from 24 to 48kHz) are encoded and losslessly buried beneath the noise floor, but underneath Area A and along with C, as shown in Fig. 8.

Fig. 9 shows the final result of Encapsulation with the components of the signal above 24kHz buried within the standard-resolution signal. The resulting file contains all the information that matters—and none that doesn’t. In fact the lossless burying is even cleverer than the illustration indicates because it provides multiple replay compatibility and streaming options. This file can be formatted as FLAC or Apple Lossless. If you play it on a DAC that lacks an MQA decoder, you’ll hear the information in Area A with better-than-CD-quality and no loss of fidelity from the presence of B or C.


But if you have an MQA decoder, the decoder will “unfold” the hidden information (Areas B and C) in two (or more) steps, to produce a high-resolution bitstream with all the information that had been inside the triangle of the high-resolution original (Figs. 10 and 11). Meridian calls this unfolding “Music Origami.” The music can be enjoyed by legacy listeners at each hierarchical step. Fig. 12 shows the fully unfolded signal with the system’s end-to-end frequency response and time behavior (low temporal blur) in the box at the top right.

As a final reflection, Bob Stuart told me that the real target is to have a coding system that does no more damage than air. Air is analog; it’s never lossless, but it is as transparent as we can get. In coding terms he equates it to an infinite sample rate, but with an 18-bit noise-floor. Actually ten meters of air introduce more temporal blur than the complete MQA encoding/decoding system, as seen in Fig. 11—a tantalizing prospect to say the least.
Conclusion
MQA accomplishes the seemingly impossible—delivering extraordinary sound quality in a form that easily integrates into the existing music distribution infrastructure, is backward compatible with existing hardware, and serves all applications, from smartphone streaming to high-end home downloads, with a single file. The combination of streaming—which is poised to become the dominant paradigm—and MQA could usher in a world in which the term “high-resolution audio” is as anachronistic as “digital camera” or “flat-panel television.” All music will be high-resolution.

By Robert Harley
My older brother Stephen introduced me to music when I was about 12 years old. Stephen was a prodigious musical talent (he went on to get a degree in Composition) who generously shared his records and passion for music with his little brother.
More articles from this editor





















